Learning Lyapunov-Stable Polynomial Dynamical Systems through Imitation
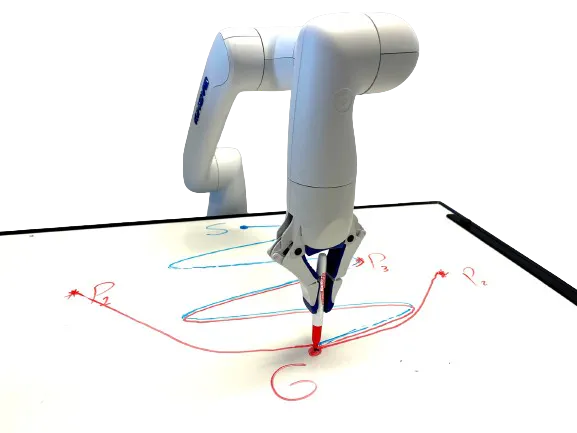 Real-world experiments on Kinova Gen3 Lite
Real-world experiments on Kinova Gen3 LiteAbstract
Imitation learning is a paradigm to address complex motion planning problems by learning a policy to imitate an expert’s behavior. However, relying solely on the expert’s data might lead to unsafe actions when the robot deviates from the demonstrated trajectories. Stability guarantees have previously been provided utilizing nonlinear dynamical systems, acting as high-level motion planners, in conjunction with the Lyapunov stability theorem. Yet, these methods are prone to inaccurate policies, high computational cost, sample inefficiency, or quasi stability when replicating complex and highly nonlinear trajectories. To mitigate this problem, we present an approach for learning a globally stable nonlinear dynamical system as a motion planning policy. We model the nonlinear dynamical system as a parametric polynomial and learn the polynomial’s coefficients jointly with a Lyapunov candidate. To showcase its success, we compare our method against the state of the art in simulation and conduct real-world experiments with the Kinova Gen3 Lite manipulator arm. Our experiments demonstrate the sample efficiency and reproduction accuracy of our method for various expert trajectories, while remaining stable in the face of perturbations.
Type
Publication
In Annual Conference on Robot Learning, 2023
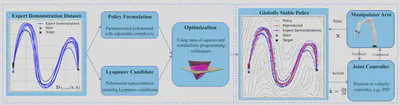
Design overview
Our method (PLYDS) benefits from trainable polynomial for both the planning policy and the safety certificate, providing adaptable complexity for different expert demonstrations.
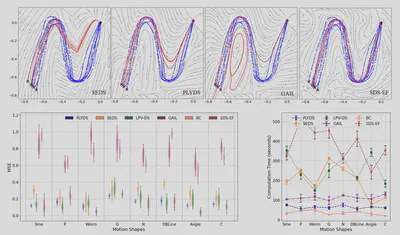
Summary of results
PLYDS is shown to improve over some baselines despite the simple formulation and computation efficiency for 2-dimensional motion planning problems.